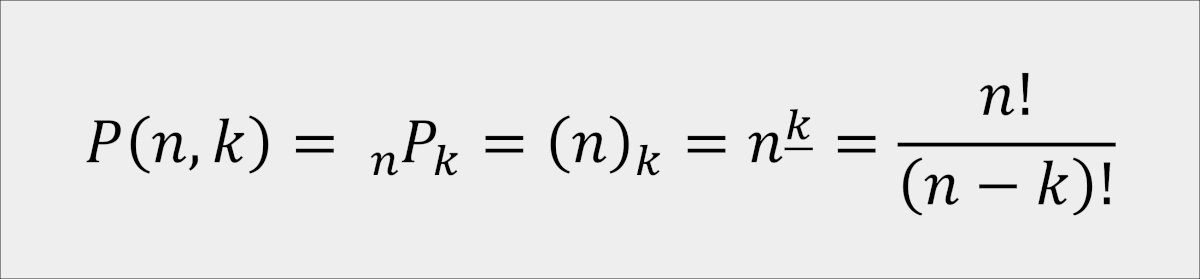
Permutations Calculator

To calculate the number of permutations, enter the number of options (n), the number of times you are allowed to choose (usually denoted as k or r), and mark the “Allow repetitions” checkbox if options can be chosen more than once. Press the “Calculate” button, and the result will be shown below.

Number of elements (n): Sequence length (k or r): Allow repetitions: Base:

Result:

2025-07-07, by

Adam has a PhD in Economics, is responsible for writing technical articles and oversees development of online applications. You can find him at:
https://narkiewicz.info/
https://www.linkedin.com/in/adamnarkiewicz/

What are permutations?

A permutation is a change to the order of elements in a sequence. The number of permutations tells you in how many different ways you can rearrange a sequence of elements.

A k-permutation of n is a way to arrange k elements from a larger set of n elements. The Permutations Calculator calculates the number of such arrangements for a given value of n and k. In some sources, the letter r is used instead of k – they mean the same thing.

k-permutations of n come in two varieties. First, they can involve sequences without replacements (repetitions); that is, each of the n elements can be used in a sequence no more than once. Second, if the elements can occur multiple times within a sequence, then we have k-permutations of n with replacements (repetitions). This calculator allows you to calculate both kinds of permutations.

Permutations and Combinations

Permutations often get confused with combinations. For example, in everyday language, you may talk about a combination of digits that opens a lock or a safe. However, strictly speaking, a sequence of digits opening a lock is most often a permutation with repetitions.

The difference between permutations and combinations, as they are defined in mathematics, is that for permutations the order of the elements matters, which is why we are talking about arrangements and sequences. On the other hand, for combinations the order does not matter, so it is more appropriate to talk about choosing elements and subsets of elements.

A code opening a lock is a sequence in which the order of digits certainly does matter, so calling it a “combination,” although common in everyday speech, is not mathematically correct.

If you are interested in combinations rather than permutations, please visit our Combinations Calculator.

The permutations formula

Let’s first consider permutations in which replacements are not allowed, that is, the k-permutations of n without repetitions. If you are building k-long sequences using n elements, the number of different sequences you can get is given by the formula

P (n, k) = \frac{n!}{(n - k)!} .

n! in the formula means the factorial of n. In addition to $P (n, k),$ some sources also use other symbols:

P (n, k) = {}_{n}P_{k} = P_{n, k} = {(n)}_{k} = n^{\underline{k}} .

On the other hand, k-permutations of n with repetitions, that is, those in which replacements are allowed, use the formula

U (n, k) = n^{k} .

This is simply n raised to the power of k.

Permutations formula explained

Imagine we need to build a sequence of length k using n elements. We can put any of the n elements at the beginning of the sequence. For permutations without replacements, the chosen element is removed from the pool, and for the second place, there are only $n - 1$ elements left. Then, the second element we choose gets removed from the available pool as well, and we have only $n - 2$ elements that can be placed in the third place. This process continues until we fill the entire sequence, resulting in the following formula:

P (n, k) = \underset{k factors}{\underset{⏟}{n \times (n - 1) \times (n - 2) \times \dots \times (n - k + 1)}} .

We can then multiply and divide this formula by the same number without changing its value. We cleverly choose $(n - k)!,$ and we get

P (n, k) = n \times (n - 1) \times (n - 2) \times \dots \times (n - k + 1) \times \frac{(n - k)!}{(n - k)!} = \frac{n!}{(n - k)!} .

For permutations with replacements, the situation is initially similar: we can choose one of the n elements for the first position in the sequence. But because repetitions are allowed, this element does not get removed from the available pool, so for the second place in the sequence, we still have n elements to choose from. Same for the third place, and so on. We make k such choices, and the final formula becomes

U (n, k) = \underset{k factors}{\underset{⏟}{n \times n \times \dots \times n}} = n^{k} .

Permutations’ examples

Question: How many permutations of a deck of cards are there?

A typical deck has 52 cards. What is the number of distinct arrangements for these cards? The total number of available elements is 52, so n = 52. The length of the sequence, that is, the number of cards we want to include in our arrangement, is also 52 because we want the arrangements of the entire deck. Therefore, k = 52. There are no repetitions because each card occurs in the arrangement exactly once. Knowing that, we have everything we need to apply the formula:

P (52, 52) = \frac{52!}{(52 - 52)!} = \frac{52!}{0!} = 52! \approx 8.066 \times 10^{67} .

This is a very large number. You can get the exact solution by using our Permutations Calculator. Because the sample size is equal to the total number of elements, that is, k = n, the formula reduces to a simple factorial, and you can get the exact answer also by calculating the factorial of 52.

Question: How many 3-letter words can I create from the word NAVY?

We have four different letters, and we want to see how many distinct three-letter arrangements we can build using these letters. Again, we can use each letter only once, so the formula is $P (4, 3) = 24 .$ Here are all 24 permutations:

NAV

NAY

NVA

NVY

NYA

NYV

ANV

ANY

AVN

AVY

AYN

AYV

VNA

VNY

VAN

VAY

VYN

VYA

YNA

YNV

YAN

YAV

YVN

YVA

Question: In how many ways can I give 7 balls of different colors to 4 children?

In this example, we want to give one ball to each of the children: Amy, Betty, Chuck, and Dale. We have seven balls: white, orange, blue, green, yellow, purple, and brown. How many different ways are there to assign one ball to each child? Again, permutations are here to help us. Since we cannot give the same ball to more than one child, we use permutations without replacements: $P (7, 4) = 840 .$

So, there are 840 ways to distribute the balls among the children.

Question: From a class of 20 students, how many ways are there to select the class president, the secretary, and the treasurer?

There are 20 people who can become the president. Let’s choose one person. Now, given that we have a president, there are 19 people who can become the secretary. And finally, once we have the president and the secretary, there are 18 people who can become the treasurer. We multiply these numbers, and we get $20 \times 19 \times 18 = 6840$ possible ways of choosing three students for these functions.

In general, whenever we have k different positions to fill and a group of n candidates, there are exactly $P (n, k)$ ways to do it. In this particular case, we have $P (20, 3) = 6840 .$

Question: How many combinations are there in a 4-digit lock if there are no zeroes?

This is not a typical lock because the digits run from 1 to 9 instead of 0 to 9. The number of elements is thus n = 9. The length of the sequence is k = 4. Each digit can be used as many times as needed, so in this case, we use permutations with replacements. The formula is

U (n, k) = n^{k} = 9^{4} = 6561 .

There are 6561 possible “combinations.” If it takes one second to check each combination, we should be able to open the lock by checking all combinations in less than two hours. Notice that the word “combinations” used in this question is not strictly correct. Because the order of the digits matters, we should be talking here about permutations with replacements, not combinations.

Question: How many passwords are there?

The answer depends on the length of the passwords and the number of available characters. As an example, we will calculate the number of passwords that are 10 characters long. We have at our disposal both small and capital Latin letters (from a to z and from A to Z – there are 52 such letters), digits (from 0 to 9), and special characters (there are 30 of them):

! @ # $ % ^ & * ( ) - _ = + [ ] \ { } | ; : ' " , . / < > ?

In total, we have 52 + 10 + 30 = 92 different characters. We can use each character as many times as we want, so we are counting the k-permutations of n with repetitions. The formula is

U (n, k) = n^{k} = 92^{10} = 43,438,845,422,363,213,824 .

This is a very large number of unique passwords. There is virtually no chance somebody is going to guess your password just by checking all possible “combinations” – as long as you picked the characters at random instead of coming up with something easy, like, for example, qwert12345 or Password0!.

Permutations in Python

If you want to calculate the number of permutations in a programming language like Python, you can use the permutations formula to create your own function:

import math
def nPk(n, k):
	return int(math.factorial(n) / math.factorial(n - k))

Similarly, you can use the formula for permutations with repetitions:

def nUk(n, k):
	return n**k

If you are interested in generating all permutations without repetitions, you can write:

from itertools, import permutations
def list_perms(n, k):
	perms = permutations(range(n), k)
	for p in perms:
		print(p)

And for permutations with replacements:

import itertools
def list_perms_with_replacents(n, k):
	for perm in itertools.product(range(n), repeat=k):
		print(perm)

Exponential calculator for large numbers

Since the formula for permutations with repetitions is $U (n, k) = n^{k},$ you can use this Permutations Calculator as an exponential calculator to calculate the power of a number. This may be convenient, especially when the result is huge (for example, you can easily get an exact value of 3¹⁰⁰⁰), because traditional calculators don’t handle big results well. Check the “Allow repetitions” box and enter the exponentiated number as n and the exponent as k. You can use only non-negative integers.

How to use the Permutations Calculator

To use this calculator, enter the number of elements to choose from in the field marked with the letter n. The sample size, that is, the length of the sequence, should be entered in the field below (marked k or r). If you are interested in permutations with replacements, check the “Allow repetitions” checkbox. Then, click the “Calculate” button to perform the calculations or the “Clear” button to re-enter the values.

The result is shown in the “Result” field below. If the result is small, it is displayed in a single line. Larger numbers are displayed in two ways: the approximation in scientific notation is shown above, and the exact number is shown below. If an error occurs during the calculations, it will be displayed instead of the result.

The calculator accepts only non-negative integers. For permutations without repetitions, the entered numbers must additionally satisfy k ≤ n. For permutations with repetitions, both numbers cannot be zero at the same time because the value of 0⁰ is indeterminate. There is no upper bound on the values you enter. You should be able to easily obtain large numbers, such as one for n = 8000000000 and k = 1000 (e.g., the number of ways to choose the top 1000 wealthiest humans from the Earth’s population). Much larger results can also be obtained, depending on your system’s configuration. However, it may take a long time to calculate a large result, or if the calculations exceed the capacity of your device, the website may crash.

You can choose the base in which you want the results to be displayed. The default is 10; that is, the results will be displayed using the decimal system. For the base, you can use any whole number from 2 to 36. However, only the results will be displayed using the selected base. The values you enter as n and k are always treated as if they were written using the decimal base.

You have an option to 1) copy the result to the clipboard, 2) download the result as a file, 3) print the result, 4) copy the link to the results to the clipboard, and 5) clear the “Result” field. To activate any of these options, use the appropriate icon above the “Result” field.

Cite or embed this content

You can use this website free of charge, including for commercial purposes, as long as you cite this website as a source. If you are citing it in a scientific text, you can use the following citation:

Narkiewicz A., Permutations Calculator, https://minesweeper.us/permutations-calculator/, accessed 2025-07-06.

To cite this website on the Internet, you can link to it using its main URL (https://minesweeper.us/permutations-calculator/) or, if you want to link to a particular result, use the “Copy link to clipboard” button.

You can also embed this page on your website using an iframe element. If you want the page to display only the calculator and hide all the remaining content (menus, article, etc.), you can use the following URL in your src attribute: https://minesweeper.us/permutations-calculator/?iframe=1.

Please credit this page on your website by citing it with a navigable link. You may also want to let us know that you have embedded our app on your website by emailing us at contact@simiade.com. Then, we will be able to inform you if we make any changes to our app that might require webmasters to update how their websites display it.

References

Charalambides, Charalambos A., Enumerative Combinatorics, CRC Press,2002.

Contact us

If you have any questions, comments, or suggestions, you can leave your feedback here:

Or you can contact us by mail:

Simiade
Adam Narkiewicz
Plac Bankowy 2
00-095 Warszawa
Poland
+48 728235409
contact@simiade.com
https://simiade.com/