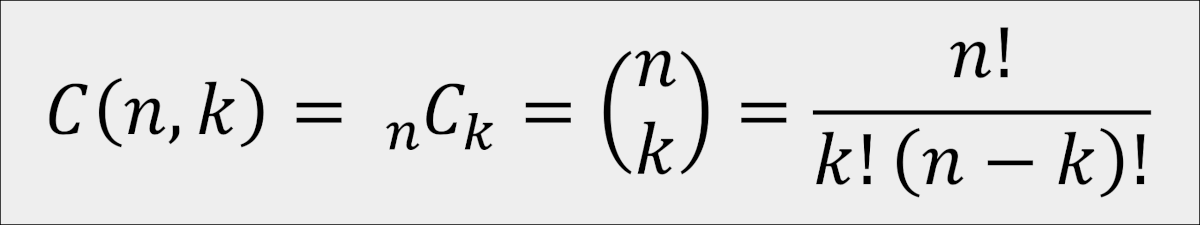
Combinations Calculator

Welcome to the Combinations Calculator. Please enter the number of elements (n) and the number of draws (k or r). Mark the box below if you allow replacements. Then press the “Calculate” button.

Number of elements (n): Sample size (k or r): Allow repetitions: Base:

Result:

2025-07-07, by

Adam has a PhD in Economics, is responsible for writing technical articles and oversees development of online applications. You can find him at:
https://narkiewicz.info/
https://www.linkedin.com/in/adamnarkiewicz/

The combinations formula

A combination tells us which k items to select from a group of n items. It is often called a k-combination of n, not to be confused with a k-permutation of n. In combinations, the order of selected items does not matter, while in permutations, it does.

How many ways are there to select k elements from a larger set of n elements? The symbol for the number of k-combinations of n without repetitions (that is when each selected element is removed from the pool so that it cannot be selected again) is $C (n, k) .$ Many sources also use symbols ${}_{n}C_{k}$ or $(\binom{n}{k}),$ with the latter being very popular. Therefore, we can write

C (n, k) = {}_{n}C_{k} = (\binom{n}{k}) = \frac{n!}{k! (n - k)!},

where n! means the factorial of n. On the other hand, the symbol for the number of k-combinations of n with repetitions (meaning selected items return to the pool and can be selected again) is $E (n, k)$ , sometimes also written as $((\binom{n}{k})) :$

E (n, k) = ((\binom{n}{k})) = C (n + k - 1, k) = \frac{(n + k - 1)!}{k! (n - 1)!} .

Combinations and permutations without repetitions are related to each other by the formula

C (n, k) = \frac{P (n, k)}{k!} .

The number of permutations is divided by k! to account for the order of items, which does not matter for combinations but does for permutations. If you are interested in situations where the order of chosen items matters, please visit our Permutations Calculator.

Combinations’ examples

How many handshakes in a group of 100?

Imagine you've just arrived at a cocktail party. There are 100 guests (including you). As you try to greet each person with a handshake, you wonder how many handshakes there would be in total if everyone greeted everyone.

There are n = 100 people. How many different pairs of people can be formed in this group? Or, in other words, how many 2-combinations of 100 are there? The answer is

C (100, 2) = (\binom{100}{2}) = \frac{100!}{2! 98!} = \frac{100 \times 99}{2} = 4950 .

There would be 4950 handshakes. Notice that we are using combinations without replacements because a person cannot have a handshake with oneself!

How many poker hands are there?

Let's consider a game without jokers; that is, our deck has 52 cards. We select five cards without replacements (because we cannot draw the same card twice). The order of the cards does not matter. Therefore, we can use k-combinations of n without replacements where k = 5 and n = 52:

(\binom{52}{5}) = 2598960 .

Therefore, there are 2,598,960 distinct hands in Poker. Knowing that we can calculate the probability of drawing any of the ranked poker hands.

Chances of getting four of a kind

To get four of a kind, we first need to select the repeated rank (13 possibilities) and then select the fifth card (48 possibilities). There are thus $(\binom{13}{1}) (\binom{48}{1}) = 13 \times 48 = 624$ different hands with four of a kind. Therefore, the likelihood of getting such a hand by chance is $\frac{624}{2598960} = \frac{1}{4165} \approx 0.024% .$

Chances of getting a full house

Calculating the chances of getting a full house is harder. First, we need to select the rank of the pair (13 possibilities) and the rank of the triplet (12 possibilities – it cannot be the same as the pair, so one option gets removed). Next, we have to account for different suit combinations. There are $(\binom{4}{2})$ suit combinations for the pair and $(\binom{4}{3})$ suit combinations for the triplet. Now, we multiply these numbers to get the overall number of possibilities:

(\binom{13}{1}) (\binom{4}{2}) (\binom{12}{1}) (\binom{4}{3}) = 13 \times 6 \times 12 \times 4 = 3744 .

There are 3744 different hands with a full house, so the probability of getting one by chance is $\frac{3744}{2598960} = \frac{6}{4165} \approx 0.144% .$ This means that getting a full house is six times as likely as getting four of a kind.

Chances of getting a flush

A flush happens when we have five cards of the same suit. We first select the suit – there are four possibilities. Then we choose five from the 13 cards of that suit: there are $(\binom{13}{5})$ ways to do it. Overall, the number of different flush hands is

(\binom{4}{1}) (\binom{13}{5}) = 4 \times 1287 = 5148 .

The probability of getting a flush by chance is $\frac{5148}{2598960} = \frac{33}{16660} \approx 0.198% .$

Chances of getting a straight

Here, we are interested in obtaining a sequence of five cards – each card is one rank higher than the previous card – regardless of their suits. To determine the number of such hands, we first need to specify the highest card. The highest card can be an Ace, King, Queen, Jack, 10, 9, 8, 7, 6, 5 (Ace can also serve as the lowest card in the 5-4-3-2-Ace sequence), so there are 10 choices for the rank of the highest card. Once we select the highest card, the ranks of all remaining cards are determined. Now we need to select the suits. There are four possible suits, and we select a suit for each of the five cards separately. We are thus using 4-permutations of 5 with replacements, for which the formula is 4⁵. Therefore, the total number of hands with a straight is

(\binom{10}{1}) \times 4^{5} = 10 \times 1024 = 10240 .

The probability of getting a straight by chance is $\frac{10240}{2598960} = \frac{128}{32487} \approx 0.394% .$

Chances of getting a straight flush

A straight flush is one of the most valued and rare poker hands. In this hand, the cards are in a sequence, like in a straight, but they are also of the same suit, like in a flush. To calculate the number of such hands, we first have to choose the highest card. As with a regular straight, there are 10 ways to do it. After the ranks of the cards have been specified, we need to select the suit, and there are four ways to do it. The final formula is

(\binom{10}{1}) (\binom{4}{1}) = 10 \times 4 = 40 .

There are only 40 such hands, so the likelihood of getting a straight flush by chance is $\frac{40}{2598960} = \frac{1}{64974} \approx 0.00154% .$

Chances of getting a royal flush

The chances of getting a royal flush are even lower than the chances of getting a straight flush. This is because the royal flush is a straight flush with an Ace as the highest card. Therefore, the ranks of cards in a royal flush are always the same: Ace, King, Queen, Jack, and 10. The only thing that can change is their suit. Since there are only four suits, there are only four hands with a royal flush. The probability of getting one is $\frac{4}{2598960} = \frac{1}{649740} \approx 0.000154% .$ This is 10 times lower than the probability of getting a straight flush.

Chances of getting three of a kind

To get three of a kind, we first have to select the rank of the triplet. There are 13 ways to do it. Then, from the remaining 12 ranks, we have to choose the ranks of the two other cards. We must ensure that we do not get a pair (otherwise, we would have a full house instead of three of a kind), so we use 2-combinations of 12 without replacements: $(\binom{12}{2}) .$ Finally, we have to select the suits. First, we pick the suits of the triplets: $(\binom{4}{3}) .$ Then, we choose the suits of the two remaining cards – and because they are of a different rank, we use 2-permutations of 4 with replacements, which gives us 4². Altogether, the formula becomes

(\binom{13}{1}) (\binom{12}{2}) (\binom{4}{3}) 4^{2} = 13 \times 66 \times 4 \times 16 = 54912 .

The probability of getting three of a kind is $\frac{54912}{2598960} = \frac{88}{4165} \approx 2.11% .$

Chances of getting two pairs

In how many different ways can we get two pairs? First, we need to select the ranks for the pairs: $(\binom{13}{2}) .$ Second, we need to choose the rank of the fifth card: $(\binom{11}{1}) .$ Third, we need to select the suits of the cards in each pair. Within each pair, cards must be of a different suit, so there are $(\binom{4}{2})$ ways to select the suits for the lower-ranked pair and $(\binom{4}{2})$ ways to select the suits for the higher-ranked pair. Finally, we must select a suit for the fifth card, and there are four ways to do so. Hence, after multiplying all these factors, we get

(\binom{13}{2}) (\binom{11}{1}) (\binom{4}{2}) (\binom{4}{2}) (\binom{4}{1}) = 78 \times 11 \times 6 \times 6 \times 4 = 123552 .

The chances of getting two pairs are $\frac{123552}{2598960} = \frac{198}{4165} \approx 4.75% .$

Chances of getting one pair

Finally, the chances of getting a single pair can be calculated as follows: 1) we choose the rank of the pair: $(\binom{13}{1});$ 2) we choose the ranks of the remaining cards: $(\binom{12}{3});$ 3) we choose the suits of the cards in the pair: $(\binom{4}{2});$ and 4) we choose the suits of the remaining three cards: 4³. You may wonder, why do we choose the ranks of the three different cards using combinations (hence $(\binom{12}{3})$ ) but their colors using permutations (hence 4³)? We must use combinations when choosing ranks because it does not matter in what order we place the cards with these ranks in our hand – if we change the order of the cards in our hand, it is still the same poker hand. However, these are three cards of different ranks, so they have their natural order – from highest to lowest. We can use this natural order to identify each card while selecting their suits. We first select the suit for the highest-ranking card. Then, we choose the suit for the middle-ranking cards. And finally, we select the suit for the lowest-ranking card. Each selection comes with four options, which gives us $4 \times 4 \times 4 = 4^{3}$ possibilities.

Therefore, the total number of hands with one pair is

(\binom{13}{1}) (\binom{12}{3}) (\binom{4}{2}) 4^{3} = 13 \times 220 \times 6 \times 64 = 1098240

and the probability of getting one pair is $\frac{1098240}{2598960} = \frac{352}{833} \approx 42.3% .$ You can verify this result experimentally. Shuffle the deck and draw five cards. Did you get a pair? Note the answer down. Repeat this process several times – you should get one pair slightly less than half the time.

What are the chances of winning the lottery?

Many countries have a lottery in which a few balls with numbers are drawn from a larger pool of balls. Whoever picks the right numbers wins – and the prizes are often very high. A popular example is Powerball. In this lottery, you need to select five numbers from 1 to 69 (without replacements) and then separately choose one more number from 1 to 26. The number of all possible combinations is

(\binom{69}{5}) (\binom{26}{1}) = 11238513 \times 26 = 292201338

Therefore, there are 292,201,338 ways to choose numbers in Powerball. In other words, you would have to buy 292,201,338 tickets to make sure you win the jackpot. If you buy only one ticket, your chances of winning are 1 in 292,201,338, which is approximately 0.000000342%.

How many ways to bring snacks to the party?

In this example, imagine that you are going to a party at your friend’s house. You were asked to contribute by bringing some snacks. There are three types of snacks: chips, cookies, and crackers. You intend to buy five bags. How many possible combinations are there?

First, we notice that there are three elements to choose from, so n = 3. Second, the order in which we arrange them does not matter. Third, we can buy more than one of each type of snack. Therefore, we should use 5-combinations of 3 with replacements. The formula is

E (3, 5) = (\binom{3 + 5 - 1}{5}) = 21 .

There are 21 ways to choose the snacks for the party. To verify that we got it right, let’s list all possible combinations (to make it short, we name the snacks A, B, and C):

AAAAA

AAAAB

AAABB

AABBB

ABBBB

BBBBB

CAAAA

CAAAB

CAABB

CABBB

CBBBB

CCAAA

CCAAB

CCABB

CCBBB

CCCAA

CCCAB

CCCBB

CCCCA

CCCCB

CCCCC

Combinations formula explained

k-combinations of n without replacements

The formula for k-combinations of n without replacements (sometimes also called the “n choose k” or “n choose r” formula) is

C (n, k) = \frac{n!}{k! (n - k)!} .

To verify whether this is indeed the correct formula, let's examine the process of selecting k numbers between 1 and n. We will start by putting the chosen numbers in a sequence of length k. The first place in the sequence can be occupied by any of the n numbers. After the number in the first place is removed from the pool, there are n − 1 options available for the second place in the sequence. This number is also removed from the pool, leaving only n − 2 numbers to choose from for the third place. We continue selecting the numbers this way until we fill the entire k-long sequence. To get the total number of such sequences (which is equal to the number of k-permutations of n without replacements), we have to multiply the number of options we have at each step:

P (n, k) = \underset{k factors}{\underset{⏟}{n \times (n - 1) \times (n - 2) \times \dots \times (n - k + 1)}} .

However, this multiplication is simply the product of the k largest factors of a factorial. Therefore, we can rewrite it as

P (n, k) = \frac{n!}{(n - k)!},

where the factorial in the denominator cancels the n − k smallest factors in the numerator so that what is left matches the previous formula.

This, however, is not the end of the story because, so far, we have calculated the number of permutations, not combinations. In permutations, the order of elements matters; we did care about the order when constructing the sequence – we chose the number for the first position, then the second, the third, and so on. Now, we want to treat all sequences that are made of the same numbers as one combination. So, how many different sequences can be made using k different numbers? The answer is easy: it is k!. There are k! as many permutations as there are combinations. To get the number of combinations, we need to divide the number of permutations by k!:

C (n, k) = \frac{P (n, k)}{k!} = \frac{n!}{k! (n - k)!} .

k-combinations of n with replacements

How do we get the formula for k-combinations of n with replacements? Each of the n elements can be selected between 0 and k times, so let’s imagine n bins numbered from 1 to n. Each bin has up to k balls in it, and the total number of balls in all bins equals k. Bins represent elements, and the balls in a given bin tell us how many times we choose the element represented by that bin.

How to describe how many balls are in each bin using a sequence of numbers? We can create a sequence of n − 1 numbers constructed in the following way: the i^th number in this sequence tells us how many balls and bins are there altogether from the first to the i^th bin. For example, the first number in this sequence is one plus the number of balls in the first bin (so it can be anything from 1 to k + 1). The second number is two plus the number of balls in the first two bins (so it can be anything from 2 to k + 2, but it has to be greater than the first number). The third number is three plus the number of balls in the first three bins (anything between 3 and k + 3 but greater than the second number). And so on. It is easy to see that the value of the last number in this sequence is n − 1 plus the number of balls in all bins except the last one. Its value can be as low as n − 1 (if all balls are in the last bin) or as high as n − 1 + k (if there are no balls in the last bin).

Now, let's change the perspective. We have a set of numbers from 1 to n − 1 + k. From this set of numbers, we select, without repetitions, n − 1 numbers. We put them in a sequence from the smallest to the largest, and now we know how many balls go into each bin. Each way of choosing n − 1 numbers from the larger pool of n − 1 + k numbers corresponds exactly to one way of distributing k balls among n bins. But how many ways are there to select n − 1 numbers, without repetitions, from a set of n − 1 + k numbers? It is

C (n + k - 1, n - 1) = \frac{(n + k - 1)!}{(n - 1)! k!} .

This is almost the formula we are looking for. The last step is to notice that we can swap the order of the factorials in the denominator, that is,

C (n + k - 1, n - 1) = \frac{(n + k - 1)!}{(n - 1)! k!} = \frac{(n + k - 1)!}{k! (n - 1)!} = C (n + k - 1, k),

and finally

E (n, k) = C (n + k - 1, k) = \frac{(n + k - 1)!}{k! (n - 1)!} .

Pascal’s triangle and binomial coefficients

A binomial is an expression involving two terms, for example, $x + y .$ Binomial coefficients are the numbers that appear next to x and y when we raise $x + y$ to a non-negative integer power. For example, ${(x + y)}^{0} = 1,$ ${(x + y)}^{1} = x + y,$ ${(x + y)}^{2} = x^{2} + 2 x y + y^{2},$ ${(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}$ – in these examples, binomial coefficients are, respectively: 1, 1-1, 1-2-1, and 1-3-3-1. It turns out that binomial coefficients are related to k-combinations of n: when we write out ${(x + y)}^{n},$ the coefficient standing next to $x^{k} y^{n - k}$ is $(\binom{n}{k}) .$ For example, in ${(x + y)}^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3},$ the coefficient standing next to $x^{2} y$ is $(\binom{3}{2}) = 3 .$ This fact can be expressed in general with the formula

{(x + y)}^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) x^{k} y^{n - k} .

Moreover, binomial coefficients form an interesting pattern – they can be arranged in a triangle, commonly known as Pascal’s triangle:

n
0						1
1					1		1
2				1		2		1
3			1		3		3		1
4		1		4		6		4		1
5	1		5		10		10		5		1
6	⋯

An interesting fact about Pascal's triangle is that the subsequent row can be formed by adding adjacent elements from the previous row. For example, the 6 in the row n = 4 comes from the 3 + 3 in the preceding row. Similarly, the 10 in the row n = 5 comes from the 4 + 6 in the row above. This observation can be summarized with the equation

(\binom{n}{k}) = (\binom{n - 1}{k - 1}) + (\binom{n - 1}{k}) .

Binomial equations and identities

Here are some of the best-known identities involving binomial coefficients:

(\binom{n}{k}) = (\binom{n}{n - k})

(\binom{n}{k}) = \frac{n}{k} (\binom{n - 1}{k - 1})

(\binom{n}{k}) = \frac{n}{n - k} (\binom{n - 1}{k})

(\binom{n}{k}) = \frac{n - k + 1}{k} (\binom{n}{k - 1})

(\binom{n}{k}) = (\binom{n - 1}{k - 1}) + (\binom{n - 1}{k})

\sum_{k = 0}^{n} (\binom{n}{k}) = 2^{n}

\sum_{k = 0}^{n} {(\binom{n}{k})}^{2} = (\binom{2 n}{n})

\sum_{k = 0}^{n} (\binom{n}{k}) x^{k} = {(1 + x)}^{n}

\sum_{k = 0}^{n} (\binom{n}{k}) x^{k} y^{n - k} = {(x + y)}^{n}

n choose k in Python

In Python programming language, to get the number of k-combinations of n without repetitions, use the comb function from the math module:

from math import comb
def nCk(n, k):
	return comb(n, k)

For the number of k-combinations of n with repetitions, use the formula relating combinations with repetitions to combinations without repetitions:

from math import comb
def nEk(n, k):
	return comb(n + k - 1, k)

If you want to display all k-combinations of n without repetitions, there is also a built-in function doing just that:

from itertools, import combinations
def list_combs(n, k):
	for c in combinations(range(1, n+1), k):
		print(c)

And to display all k-combinations of n with repetitions, use:

from itertools import combinations_with_replacement
def list_combs_wr(n, k):
	for c in combinations_with_replacement(range(1, n+1), k):
		print(c)

If you want to write your own function for the number of k-combinations of n without repetitions, here is an example:

from math import factorial
def nCk(n, k):
	return int(factorial(n) / (factorial(k) * factorial(n-k)))

And for a function calculating the number of k-combinations of n with repetitions, you can use:

from math import factorial
def nEk(n, k):
	return int(factorial(n + k - 1) / (factorial(k) * factorial(n-1)))

How to use the Combinations Calculator

The Combinations Calculator allows you to calculate k-combinations of n with and without repetitions. To perform a calculation, enter the number of available elements in the field marked with the letter n. Then, enter the number of draws in the field marked with k or r. If you are interested in combinations with repetitions, mark the checkbox below. Finally, press the “Calculate” button, and the results will be displayed below.

The Calculator is particularly well suited for calculations involving very large numbers. Calculating the result for inputs such as n = 1000000 and k = 1000 will not be a problem. For big numbers, the Calculator shows the result in two forms. In the first line, it displays an approximation in scientific form, and in the second line, it displays the exact solution.

There are no preset limits, and the Calculator attempts to perform calculations regardless of the size of n and k. Whether the calculations are successful depends on the configuration of your system. Modern versions of the Chrome browser on desktop computers can easily compute the results for inputs such as n = 8000000000 and k = 10000000 (how many ways to select 10,000,000 survivors to live on a giant spaceship after an asteroid impact destroys the Earth?). However, other system configurations, especially on mobile devices, may struggle with numbers that large.

The Calculator has several other features. You can:

Select the base in which you want the results to be displayed. You can use any whole number from 2 to 36. The default base is 10; that is, by default, results are displayed using the decimal system. If you select a different base, it will be used only to display the results. The input is always read using base 10.
Clear the field with n and k by clicking the “Clear” button. Then, you can reenter the desired values.
Copy the result to the clipboard. To use this feature (and all the following features), press the appropriate button above the “Result” field.
Download the result and save it to your device in a text file.
Print the result.
Copy the link to the result to the clipboard.
Clear the result.

Cite or embed this content

You can use this website free of charge, including for commercial purposes, as long as you cite this website as a source. If you are citing it in a scientific text, you can use the following citation:

Narkiewicz A., Combinations Calculator, https://minesweeper.us/combinations-calculator/, accessed 2025-07-06.

To cite this website on the Internet, you can link to it using its main URL (https://minesweeper.us/combinations-calculator/) or, if you want to link to a particular result, use the “Copy link to clipboard” button.

You can also embed this page on your website using an iframe element. If you want the page to display only the calculator and hide all the remaining content (menus, article, etc.), you can use the following URL in your src attribute: https://minesweeper.us/combinations-calculator/?iframe=1.

Please credit this page on your website by citing it with a navigable link. You may also want to let us know that you have embedded our app on your website by emailing us at contact@simiade.com. Then, we will be able to inform you if we make any changes to our app that might require webmasters to update how their websites display it.

References

Charalambides, Charalambos A., Enumerative Combinatorics, CRC Press,2002.

Contact us

If you have any questions, comments, or suggestions, you can leave your feedback here:

Or you can contact us by mail:

Simiade
Adam Narkiewicz
Plac Bankowy 2
00-095 Warszawa
Poland
+48 728235409
contact@simiade.com
https://simiade.com/